
When I started programming for Data Science related projects, it took a little bit of catching up to understand the proper representation of multi-dimentional arrays in Python programming language. So I thought I’ll write an article about it, hoping that it’ll help anyone looking for some guidance.
The scalar, vector and matrix respresentation in Python is key to the learning process in understanding the Linear Algebra for Data Science.
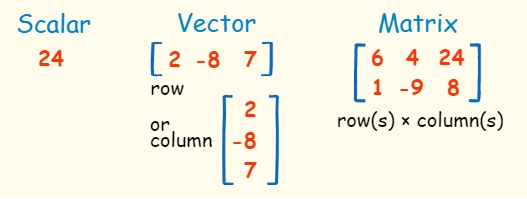
Scalar
A numeric value, representing an integer in the space is considered as a Scalar. It is represented in lower case. A scalar when multiplied by a vector value literally transforms the vector into the a vector times that of scalar
Example
- Scalar is represented as a lower case - a, n etc.
- When you multiple a vector with a scalar i.e., n . $\mathcal{V}$ = n $\mathcal{V}$
Vector
A vector is similar to an Array. A vector holds multiple number values. In Python, you can do operations on vectors using things such as dot product and cross product, just like in linear algebra. These operations are used to efficiently manipulate data in computation processes.
Creating vectors in Python using numpy libraries.
I am assuming you have installed python on your machines. Pull up a notepad or a text editor and start by creating a file. Name the file as you wish, but with an extension with .py
Below is the code that’ll help you create a column vector in python.
# Load library
import numpy as np
# Create a vector as a row
vector_row = np.array([1, 2, 3])
# Create a vector as a column
vector_column = np.array([[1], [2], [3]])
print(vector_column)
Now, save the file and pull up your command prompt if you are on Windows OS, or Shell for Linux OS, or Terminal for MacOS.
To execute the file, type below commands. Replace the filename with the name of the file that you have choosen in the above step.
$python vec-in-python.py
Output
[[1],
[2],
[3]]
That’s how you create a vector in Python.
Matrices
In the study of systems of linear equations, the properties of the data i.e., the metadata of the data can be represented in the form of a matrix. A rectangular array of numbers is called a matrix (the plural is matrices), and the numbers are called the entries of the matrix. Matrices are usually denoted by uppercase letters: A, B, C, and so on.
For instance, you go to a grocery store and buy two items of $i$ and three items of $j$, the total costed you $10$ dollars. You bought the same items the other day, except now the quantity is different and the total cost if different. We would like to represent this in the form of a Matrix, so that we can solve for the price of individual items $i$ and $j$.
Let’s try creating a Matrix.
# Load libraries
import numpy as np
# Create a matrix
matrix = np.array( [[2, 3],
[4, 1]] )
# Create compressed sparse row (CSR) matrix
print(matrix)
Here’s how the output would look like if you were to print it in the shell.
$python mat-in-python.py
Output
[[2 3]
[4 1]]
That is the representation for two items $(i, j)$ bought on day one for $2$ dollars and $3$ dollars respectively. And on the day two, the same items costed $4$ and $1$ dollar respectively. Hope that helps!